Ce este aria triunghiului isoscel. Matematica este una dintre acele materii care dau mari batai de cap elevilor, atat in scoala primara, cat si in gimnaziu sau la liceu. Trebuie sa recunoastem, nu toti elevii reusesc sa invete bine la matematica. Daca algebra mai este cum este, geometria este si mai grea de inteles pentru multi elevi.
Nu e de mirare asadar ca multi ajung in situatia de a nu reusi sa rezolve anumite exercitii simple in cadrul examenelor. Spre exemplu, la ultima evaluare nationala, multi elevi au fost incurcati de un exercitiu in care trebuia calculata aria unui triunghi isoscel. Asadar, haideti sa ne reamintim impreuna ce este, de fapt, aria triunghiului isoscel si cum se calculeaza aceasta!
Ce este un triunghi isoscel
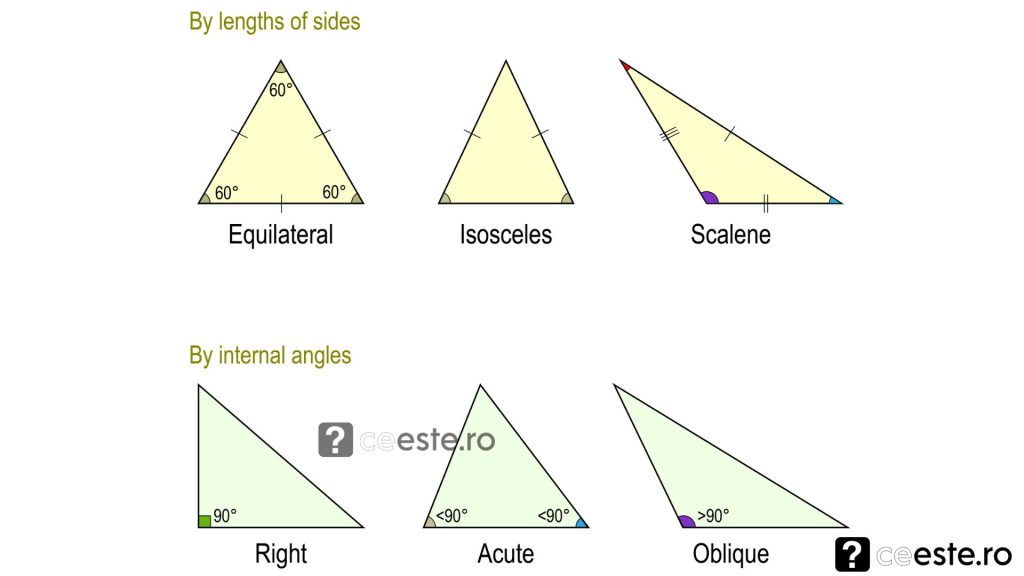
Inainte de a porni la treaba, trebuie sa spunem ca stim despre aria unei suprafete ca este o masura a cat de intinsa este de fapt acea suprafata. In cele mai multe cazuri, cuvantul “suprafata” este utilizat cu sensul de “arie”.
Atunci cand vorbim despre matematica, aria este un numar real, in general pozitiv. Unitatea de masura pentru arie in Sistemul International este matrul patrat, avand simbolul “m2”. Sigur, aria poate avea asociata uneori si o unitate de masura, insa asta se intampla atunci cand vorbim despre fizica, inginerie, geodezie, etc.
In primul si primul rand, trebuie sa definim ce este triunghiul isoscel. Asa cum probabil ca cei mai multi dintre voi va amintiti, potrivit definitiei generale, triunghiul isoscel este acel triunghi care are doua laturi congruente, adica egale, in timp ce cea de-a treia latura serveste drept baza. Practic, daca vorbim despre un triunghi ABC, vom avea o baza BC si doua laturi congruente AB si AC, de lungime egale.
Citeste si: Ce este mediana si ce determina
Poate ca va intrebati acum de unde provine aceasta denumire a triunghiului isoscel, nu-i asa?! Ei bine, termenul “isoscel” provine din limba greaca, fiind format din alaturarea a doua cuvinte: “isos”, care inseamna “egal”, respectiv “skelos”, care inseamna “picior”. Cele doua laturi congruente despre care aminteam in randurile anterioare au aceeasi lungime si sunt considerate “picioarele” triunghiului isoscel.
Triunghiul isoscel are cateva proprietati specifice, care il diferentiaza de alte triunghiuri. Spre exemplu, stim foarte clar ca daca un triunghi este isoscel, atunci unghiurile de la baza sa sunt congruente. Reciproc, daca un triunghi are doua unghiuri congruente, atunci este vorba despre un triunghi isoscel.
Mai departe, bisectoarea unghiului opus bazei unui triunghi isoscel este totodata inaltime, mediana si mediatoare. De asemenea, in orice triunghi isoscel, mediatoarea bazei triunghiului este intotdeauna si axa de simetrie a triunghiului. Apoi, inaltimea corespunzatoare bazei este si mediana, si mediatoare, dar si bisectoare a unghiului opus bazei.
Ce este aria triunghiului isoscel
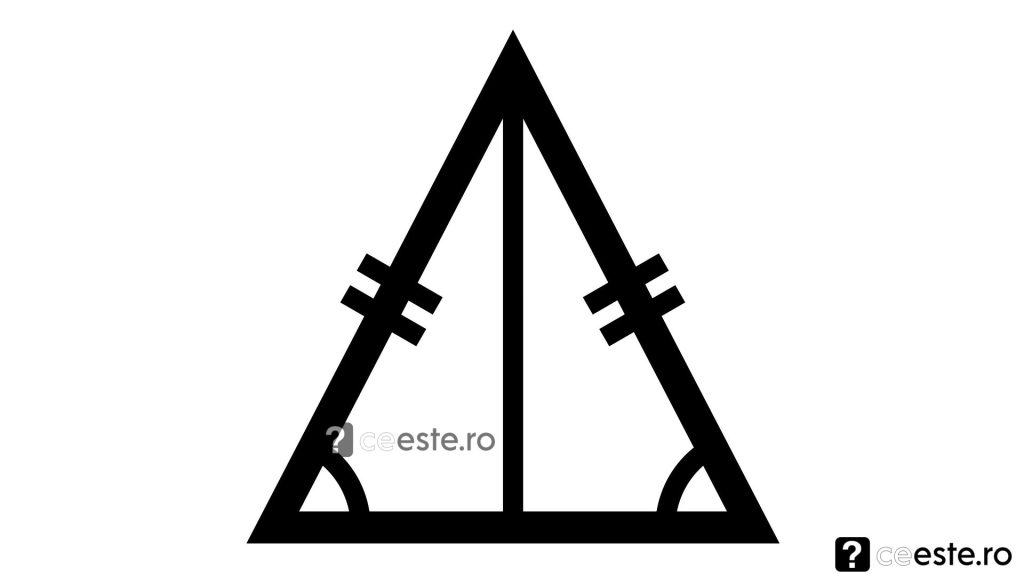
Mai departe, atunci cand vorbim despre un triunghi isoscel mai stim intotdeauna ca medianele duse din varfurile bazei sale sunt congruente. De asemenea, si inaltimile duse din varfurile bazei sunt congruente. Nu in ultimul rand, bisectoarele duse din varfurile bazei sunt, de asemenea, congruente.
In cazul in care avem un triunghi isoscel cu un unghi de masura de 60 de grade, inseamna ca vorbim despre un triunghi echilateral. In cele din urma, mai spunem ca in cazul unui triunghi isoscel, medianele, bisectoarele si inaltimile duse din varfurile bazei nu coincid.
Sa revenim acum la problema de la care am pornit, si anume metoda prin care se poate calcula aria unui triunghi isoscel. Formula implica urmatoarele doua notiuni: baza si inaltime (aceasta fiind si mediana si mediatoarea si bisectoarea intr-un triunghi isoscel).
Prin definitie, aria unui triunghi este b x h impartit la 2, unde b reprezinta lungimea unei laturi, iar h lungimea inaltimii corespunzatoare acelei laturi. Avem asadar urmatoarea formula extrem de simpla cu ajutorul careia se poate calcula aria unui triunghi isoscel: A = , unde A = aria, b = baza, h = inaltimea.